Auteur : Jean-Pierre Lubet
Compte-rendu d’un atelier réalisé durant un stage PAF en 2018-19 enrichi de figures interactives de l’atlas EMTA.
En complément à cet article, on peut lire aussi l’article Géométrie du cadastre et enseignement, hier et aujourd’hui.
Sommaire
Le rayon de la Terre : quelques travaux anciens
La mesure d’un arc de méridien par Picard
La méridienne vérifiée par Jacques et César-François Cassini
Géométrie, analyse, théorie des probabilités
La mesure du rayon de la Terre par Eratosthène est en général bien exploitée dans les manuels scolaires. Mais d’autres méthodes ont été utilisées. En particulier, aux XVIIème et XVIIIème siècles, plusieurs séries de mesures géodésiques ont été effectuées en France dans le but de mesurer le rayon de la Terre et de préciser la carte de France. L’objectif de l’atelier organisé pendant le stage de l’année 2018-2019 était de mettre en évidence des situations géométriques simples sous-jacentes à ces travaux et de les illustrer, lorsque c’était possible, par des relevés qui concernent la région septentrionale de la France. Il s’agissait notamment d’explorer les documents historiques disponibles sur ce sujet, avec la perspective d’une exploitation possible dans certaines classes de collège et de lycée.
Le rayon de la Terre : quelques travaux anciens
Parmi les méthodes mises en œuvre pour évaluer le rayon de la Terre, celle d’Eratosthène est souvent représentée dans les manuels scolaires. On sait que le savant a considéré les villes de Syène (aujourd’hui Assouan) et d’Alexandrie le jour du solstice d’été (fig. 1).
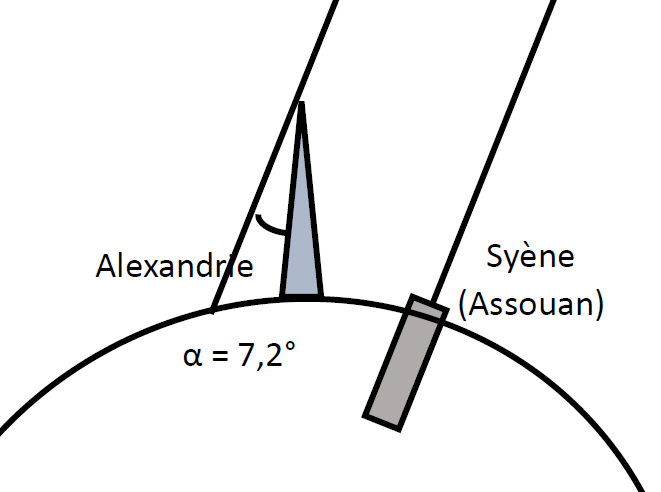
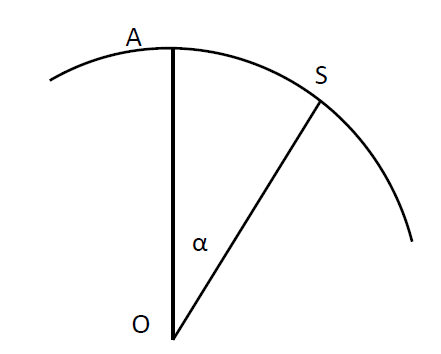
Ce jour-là, à midi, le soleil éclaire le fond d’un puits à Syène, il est à la verticale de ce lieu ; au même moment à Alexandrie l’ombre portée par un obélisque permet de mesurer l’angle α entre les rayons du Soleil et la verticale du lieu. On en déduit que les rayons de la sphère terrestre qui aboutissent respectivement à Alexandrie et à Syène font entre eux un angle α (fig. 2). La distance séparant les deux villes est alors la mesure de l’arc AS, elle est estimée à 5000 stades (soit 820 km). La circonférence, puis le rayon OS s’en déduisent aisément :
On trouvera dans [Bresinski] des indications sur d’autres travaux géodésiques réalisés par les Grecs puis les arabes.
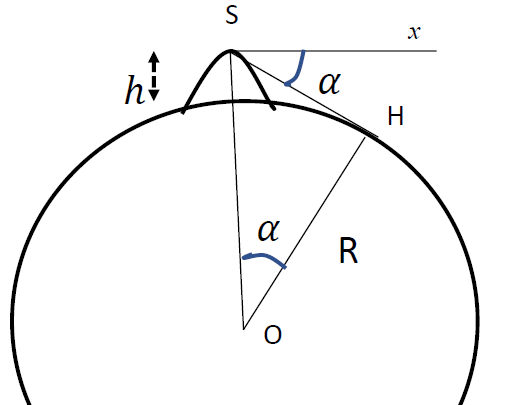
Mais la méthode décrite par Biruni (973-1050) est peu connue. Elle ne repose pas sur la connaissance d’une distance à la surface du globe, mais elle suppose connue la hauteur h d’une montagne. Il faut que cette montagne soit proche d’un rivage marin ou d’une plaine sans relief [Al Biruni, p. 183-189]. Au sommet S, on détermine la verticale SO (par l’équivalent d’un « fil à plomb ») et l’horizontale Sx (fig. 3). En visant l’horizon selon SH, on peut évaluer l’angle α = xOH. Dans le triangle OSH on peut alors écrire
Biruni rend compte d’une mesure effectuée au nord-est de l’actuel Pakistan, pour une attitude équivalente à h=321,46 m, et un angle α = 0°34’, le calcul fournit une valeur de R =6335 km.
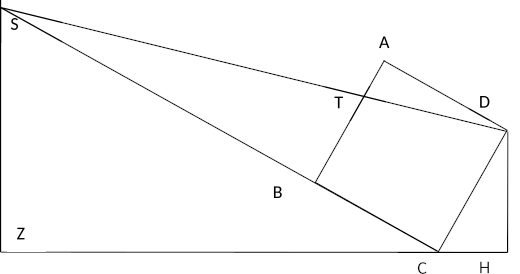
Pour mesurer l’altitude h d’un sommet, Biruni donne une méthode originale, fondée sur l’utilisation d’un cadre rigide de forme carrée ABCD, de côté c (fig. 4). Le cadre est dressé dans un plan vertical de façon à réaliser l’alignement des points B, C, S. Au sommet D est fixée une alidade mobile autour du point D par laquelle on vise le sommet S, on marque ainsi le point T où la droite DS coupe le côté AB du carré. La mesure des segments AT et CH permet de calculer la hauteur h=SZ. La similitude des triangles SCD et DAT permet en effet d’écrire :
De même les triangles SZC et CHD sont semblables et l’on a
Finalement
Et l’altitude cherchée peut s’écrire
A la Renaissance, en France, on notera la mesure effectuée par Jean Fernel, astronome et médecin du roi Henri II (1506-1558). Elle est fondée sur la distance entre les cathédrales de Paris et d’Amiens, situées sur un même méridien. Par des observations du soleil, l’arc entre ces points est estimé à un degré. La distance qui les sépare est évaluée en comptant les tours de roue lors d’un voyage en voiture, et en opérant les corrections pour tenir compte des détours d’un chemin qui n’est pas rectiligne. Il trouve 56746 toises, soit environ 110 km. Ce qui donne un rayon terrestre de 6300 km. Etant donné le procédé utilisé, on peut penser que le hasard a bien fait les choses.
Le principe de la triangulation
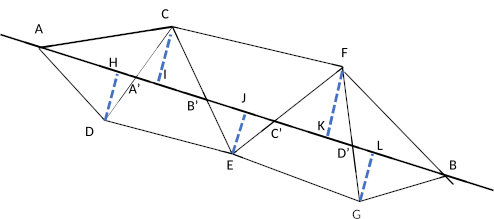
Mais les mesures – imprécises – de longues distantes vont être abandonnées avec le développement de la méthode de triangulation. Celle-ci est utilisée par le Hollandais Willebrord Snell Van Royen, dit Snellius (1580, 1626). En 1621, il mesure un arc de méridien de 1°11′. La seule distance effectivement mesurée sur le terrain est une « base » de 1230 mètres. Les autres distances recherchées s’en déduisent au moyen d’une chaîne de triangles dont les angles sont relevés minutieusement.
La figure 5 illustre le principe de la méthode. Il s’agit de mesurer la distance AB. Une fois la base AC connue, des mesures d’angles et les relations trigonométriques dans le triangle permettent de déterminer successivement les longueurs AA’, A’B’, B’C, C’D’ et D’B et donc finalement la distance AB. Le résultat peut aussi être obtenu en calculant les longueurs AH, HI … obtenues en projetant sur AB les côtés de la chaîne de triangles.
Le détroit du Pas de Calais
La triangulation permet évidemment de mesurer des distances entre des lieux séparés par quelque obstacle infranchissable. Ainsi Picard indique comment il a évalué la largeur du Pas de Calais :
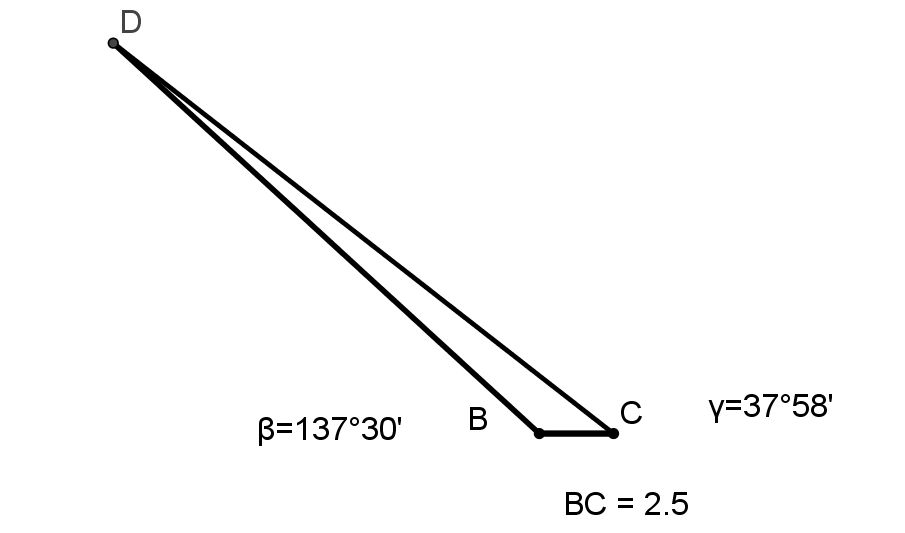
Par l’occasion des grands Instruments que l’on avoit portez à calais, on voulut déterminer la distance qu’il y a entre ce Port et le Château de Douvre en Angleterre, que l’on peut voir assez clairement, quand le Ciel est devenu serein. Le 20 Novembre au matin, la Mer étant fort basse, nous mesurâmes sur la Greve du Port de Calais qui regarde les Côtes d’Angleterre, une ligne droite de 2500 toises, en commençant à la pointe du Bastion du Risban, qui est du côté de la Mer nous prîmes l’angle que la base mesurée faisait avec le milieu des deux Tours les plus apparentes du Château de Douvre que nous trouvâmes de 37°58’, & ayant transporté l’Instrument à l’autre extrémité de la base vers Boulogne, nous mesurâmes l’autre angle que nous trouvâmes de 137°30’, donc l’angle restant du triangle qui avoit son sommet au Château de Douvre étoit de 4°32’, d’où il s’ensuit que la distance entre la pointe du Bastion du Risban & le Château de Douvre est de 21360 toises, mesures du Châtelet de Paris.
[Picard et La Hire 1719, p. 410-411]
Avec ces données on peut tenter une évaluation de la distance Calais -Douvres en construisant à l’échelle le triangle BCD, dont on connaît le côté BC et les angles de sommets B et C (fig. 6). On constate vite que la mesure de CD est très sensible aux petites variations des angles. Ce manque de précision, sensible lors d’un tracé sur papier, affecte aussi la fiabilité du résultat obtenu par les calculs.
On retrouve aussi une illustration de ces visées dans l’atlas EMTA (année 1681)
Quelle forme pour les triangles ?
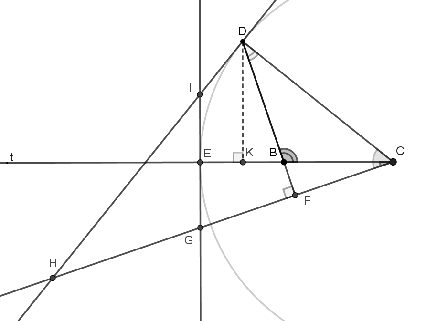
Pierre Bouguer (1698-1756) a étudié cette question par des moyens géométriques dont on va donner maintenant la substance. Pour calculer la distance DC, on décide d’utiliser une base BC portée par une demi-droite Bt donnée (fig. 7). Il s’agit de déterminer la longueur que l’on doit donner à cette base pour obtenir la valeur de DC avec l’incertitude la plus faible possible.
La relation des sinus dans le triangle BCD permet de calculer :
On suppose que les erreurs sont dues aux seules mesures des angles, et l’on ne tient pas compte des erreurs possibles sur la mesure de la base BC. L’incertitude relative sur le calcul de DC est donc :
On suppose que l’incertitude absolue est la même sur la mesure des deux angles. Le problème revient donc à rendre minimale l’expression :
Soit alors le cercle de centre C et de rayon CD, il coupe la demi-droite Ct en E. Les tangentes en E et D au cercle se coupent en I. La perpendiculaire issue de C à la droite BC coupe BC en F et les tangentes précédentes en G et H. Le recours à des angles complémentaires dans les triangles rectangles DFC et BFC permet d’écrire le résultat :
Les deux angles sont respectivement inclus dans les triangles rectangles ECG et DCH :
Finalement, si l’on note R la distance DC on obtient
On peut alors suivre les variations de δ en imaginant que le point B s’éloigne du point C. Les longueurs EG et DH décroissent simultanément jusqu’à ce que le point G se confonde avec le point K, projection orthogonale de D sur Ct. Puis, B se rapprochant de E (fig. 8), HD continue de décroître tandis que GE croît, mais tant que le point G n’a pas atteint le point I les accroissements de GE sont inférieurs aux diminutions de DH. Ensuite, quand B s’éloigne de E sur la demi-droite GE augmente plus rapidement que DH diminue et δ se remet à croître. Finalement la quantité δ passe par un minimum quand G et H sont confondus avec I, c’est-à-dire quand BC=BE = DC. Bouguer conclut en caractérisant le triangle BCD optimum :
II faut le plus qu’on peut, rendre le triangle isoscele, ou faire la base que l’on doit mesurer de même longueur que l’autre ligne.
[Bouguer 1749, p. 87].
La mesure d’un arc de méridien par Picard
En France, lorsque l’Académie des Sciences est créée par Colbert en 1666, l’une des premières tâches qui lui est assignée est la réalisation d’une carte de France.
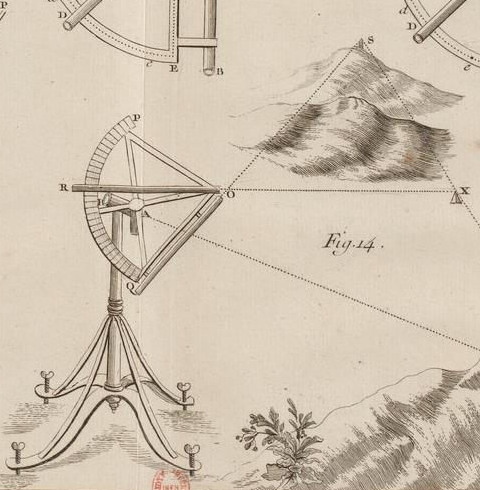
Au XVIIème siècle, pour la mesure des angles sur le terrain, l’instrument est le quart de cercle (fig. 9). Il est composé d’un limbe en quart de cercle, et de deux instruments de visée appelés alidades, l’un, QO, est solidaire du limbe, l’autre, RO, peut pivoter autour du centre O du cercle. Pour mesurer l’angle SOX on place le quart de cercle de façon à réaliser l’alignement QOS, puis on fait pivoter l’alidade mobile pour réaliser l’alignement ROX. Les graduations du limbe permettent alors de lire une mesure de l’angle à évaluer. La précision de la mesure est d’autant meilleure que le rayon du quart de cercle est grand. Cependant la taille reste limitée car l’instrument doit pouvoir être transporté, y compris dans des lieux difficiles d’accès (sommets, clochers, tours, …).
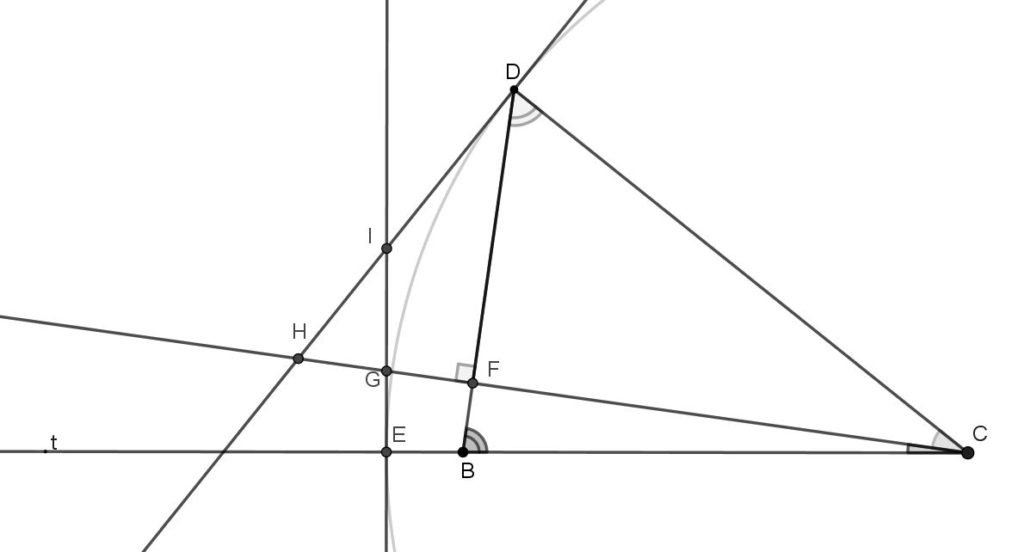
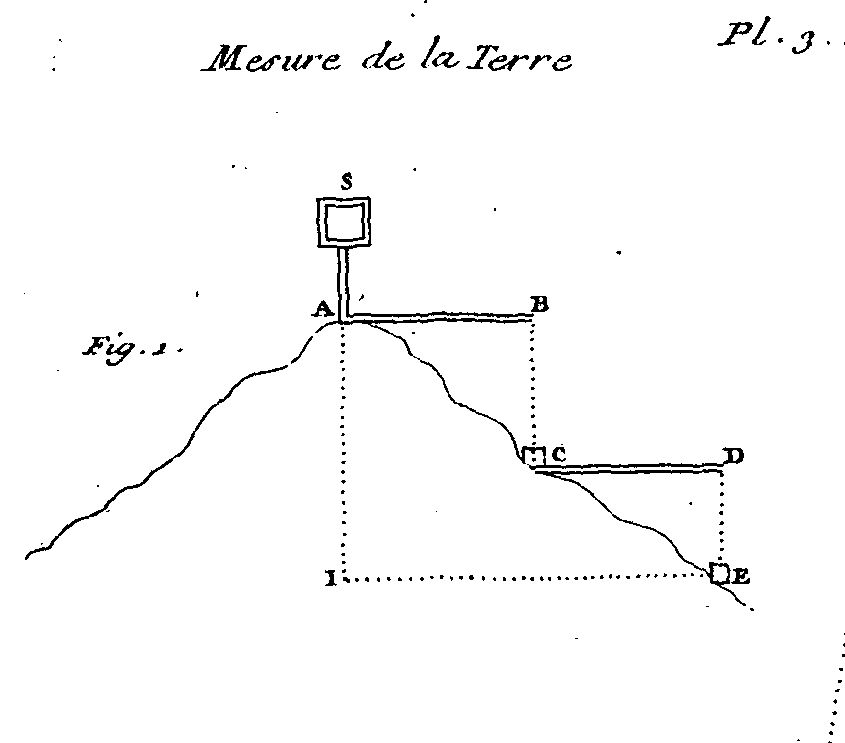
Initialement, chaque alidade est munie de deux pinnules, c’est-à-dire de deux orifices permettant d’effectuer la visée (fig. 10). L’astronome Jean Picard (1620-1682) a l’idée de remplacer ces pinnules par une lunette astronomique. Dans la lunette un cadre actionné par un micromètre permet de déplacer un cheveu (ou réticule), permettant des visées encore plus précises. C’est lui qui va réaliser les premiers travaux géodésiques pour l’Académie. Il va d’abord mesurer un arc de méridien de. L’arc doit joindre les villages de Sourdon, près d’Amiens, et de Malvoisine, près de la Ferté-Alais.
Une base est mesurée près de Paris (fig. 11), elle fait 5663 toises (à peu près 11 km), entre le moulin de Villejuif et le Pavillon de Juvisy. Une chaîne de triangles est ensuite constituée pour relier les extrémités de l’arc, une observation complémentaire finira même par inclure la station constituée par la cathédrale d’Amiens.
fig.11
Pour la mesure des angles, le quart de cercle utilisé a un rayon de 38 pouces (1,03 m), il est gradué en minutes. Par exemple, pour le premier triangle (Villejuif‑Juvisy‑Brie-Comte-Robert, soit ABC, fig. 12) les mesures angulaires suivantes ont été retenues
fig. 12
Le côté AB a été mesuré directement et la relation des sinus permet de déterminer les deux autres côtés :
Ce dernier résultat va permettre de déterminer les côtés AD et CD du triangle dont les sommets sont Villejuif Brie-Comte-Robert et Montlhéry, et ainsi de suite.
fig. 13
Le segment GI (Mareuil-Clermont) fait l’objet d’un traitement spécifique (fig. 13). A la station de Mareuil, Picard observe l’étoile polaire et il détermine ainsi l’angle du côté GI avec la méridienne (1°9’). De la longueur de GI, il peut alors déduire la distance Iθ qui sépare les parallèles de Clermont et de Mareuil :
Puis comme les angles de tous les triangles de la chaîne sont connus, l’inclinaison de GI sur la méridienne permet de calculer l’inclinaison des côtés NV, NI, et GE et finalement de calculer la longueur de l’arc de méridien joignant Malvoisine au parallèle d’Amiens [Picard, p. 16].
Picard note que ces calculs ne tiennent pas compte de la sphéricité de sphère, mais que le résultat ne doit pas en être affecté :
Bien qu’en effet les 4 lignes dont cette distance est composée, soient comme les côtez d’un Polygone qu’on auroit voulu décrire à l’entour de la Terre , & que dans la rigueur de la Géometrie, il soit vrai que le contour d’un tel polygone seroit plus grand que la circonférence de la terre ; il y a néanmoins si peu de différence en cette rencontre, qu’il seroit inutile d’y avoir égard puisque l’excès sur chaque degré ne monteroit pas à la valeur de l3 pieds, de sorte que qu’on peut considerer toutes ces lignes particulieres dont la distance Nα est composée comme insensiblement differentes de la courbure d’un Méridien.
[Picard, p. 16]
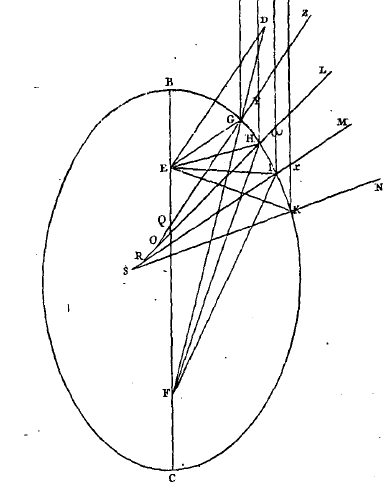
Outre les opérations de triangulation proprement dites, des observations astronomiques doivent déterminer les coordonnées géographiques des différentes stations. La précision requise est supérieure à celle que donne le quart de cercle dont le rayon dépasse à peine un mètre. Picard concevra à cet effet un secteur de 18° et de plus de trois mètres de rayon (fig. 13). Par exemple, on mesure la distance zénithale bBX d’une étoile au point B, puis la distance zénithale de la même étoile en un point C sur même méridien, par différence on obtient alors la différence de latitude CAB des points B et C (fig. 15).
Commencée fin 1668, la triangulation est achevée en 1670. Elle donne la longueur moyenne de 57 060 toises (111,21 km) pour un degré (soit une circonférence de 40 035 km).

Le compte rendu qui en est donné en 1671 montre que de nombreuses précautions ont été prises pour assurer aux mesures angulaires la meilleure précision possible. Un même angle est mesuré plusieurs fois, et par des observateurs différents. Les résultats sont donnés à 10 secondes près. Pour un triangle donné, les trois angles sont dûment mesurés ; malgré toutes les précautions prises, il arrive que la somme ne fasse pas exactement 180°. C’est ce qu’on appelle l’« erreur de fermeture ». Dans ce cas, à partir des conditions d’observation, Picard corrige l’un des angles qui ne lui semble pas aussi « assuré » que les deux autres, et sur lequel il rejette la faute [Picard, p. 8]. Pour l’une des stations, on pourrait être tenté de réitérer les mesures, mais Picard invoque les difficultés de l’entreprise : l’enjeu ne mérite pas que l’on s’expose à nouveau au danger d’escalader une « tour à moitié ruinée » [Picard, p. 11].
Cette mesure du méridien est ensuite complétée par des relevés qui aboutissent en 1678 à la publication d’une carte des environs de Paris qui s’étend sur une centaine de kilomètres du nord au sud.
La mesure du méridien par Giovanni-Domenico et Jacques Cassini, la controverse sur la figure de la Terre
Colbert souhaite une carte complète du royaume. Dans un rapport de 1681, Picard trace un programme de travail dont le premier objectif serait de prolonger la chaîne de triangles initiale et d’effectuer une mesure du méridien entre Dunkerque et Perpignan. Picard meurt en 1682, Colbert charge Giovanni Domenico Cassini (1625-1712) de ce travail. Celui-ci, né dans le comté de Nice, a inventé une méthode de mesure des longitudes fondée sur l’observation des satellites de Jupiter, il a rejoint l’Académie des sciences dès 1669, il a été chargé de la construction de l’Observatoire de Paris. Premier d’une lignée d’astronomes occupant cet Observatoire, il sera souvent nommé Cassini 1er.
Deux équipes se dirigeant l’une vers le Nord, l’autre vers le Sud commencent les relevés. Mais changements des priorités, assèchement des caisses de l’état : les travaux sont plusieurs fois interrompus et les derniers relevés ne sont effectués qu’à partir de 1718. C’est le fils de Giovanni Domenico qui est cette fois à l’œuvre : Jacques dit Cassini II (1677-1756). Il rassemble les résultats dans un mémoire publié en 1720.
Dans la partie septentrionale, on ne rencontre pas de massif montagneux, pour autant les relevés ne sont pas toujours faciles :
Nous avons fait transporter nos quarts de cercle dans les Tours ou Clochers, dont la situation étoit la plus avantageuse pour la continuation des Triangles, & comme, dans la Picardie, l’Artois & la Flandres, la plupart de ces Clochers sont environnés d’arbres très élevés, il a fallu s’y placer le plus haut qu’il a été possible, y dresser des échafauts, & y faire des ouvertures en différents endroits, pour pouvoir découvrir les objets éloignés qui étoient aux environs.
[Cassini II 1720, p. 191]
Toutefois, à l’extrémité nord de la chaîne de triangles, les vastes plages de sable vont offrir un terrain satisfaisant pour mesurer une nouvelle base et contrôler ainsi les résultats obtenus.
L’une des extrémités de la base sera signalée par le pignon d’un fort en ruine – le Fort du Revers proche du port de Dunkerque. Au nord-est, à l’autre extrémité, près de la frontière du royaume, une dune va servir de repère, elle avance plus que les autres en direction de la mer et elle peut être reliée à Dunkerque par une ligne droite en suivant la plage, un signal est construit à son sommet, duquel on peut viser les stations utilisées précédemment : la tour de Dunkerque (dite du Leughenaer), le clocher de Hondschoote, le Mont Cassel … La mesure de la base est faite sur la plage à l’aide de perches déplacées horizontalement. L’extrémité orientale est la projection orthogonale I du signal sur le plan horizontal du rivage. Cassini décrit avec précision l’opération réalisée pour tenir compte du relief de la dune : la première perche est placée en position horizontale au sommet de la dune en direction du Fort du Revers, à son extrémité un fil à plomb permet de situer le point C où l’on va établir la seconde perche CD … (fig. 16). Le même type d’opération est mis en œuvre au Fort du Revers, à l’autre extrémité.
Dans son rapport final, Cassini II indique combien ces travaux ont été précieux pour une élaboration correcte d’une carte du royaume. Ils ont permis de donner avec exactitude les lieux traversés par le méridien de Paris et de rectifier, de préciser la distance de nombreuses villes par rapport à ce méridien. Mais, la publication du rapport intervient dans un contexte très particulier : partisans et adversaires de la théorie de Newton sur la gravitation universelle s’affrontent au sein même de l’académie. Une question suscite des controverses passionnées. Selon Newton, la Terre doit avoir la forme d’un ellipsoïde aplati aux pôles.
Les résultats obtenus par Cassini II donnent une longueur moyenne de 57097 toises pour un degré de méridien entre Paris et Collioure, contre 56960 entre Paris et Dunkerque. Cassini II peut affirmer :
Ainsi il paroît avec assés d’évidence que les degrés d’un Méridien sont plus grands, plus ils sont prés de l’Equateur, & diminuent, au contraire, à mesure qu’ils s’approchent du pole. [Cassini II, p. 237]
[Cassini II, p. 237]
S’appuyant sur une figure montrant de façon précise les arcs associés à des rayons de courbure de plus en plus grands lorsqu’on s’approche de l’Equateur, il précise :
[La surface de la Terre ] doit avoir la figure d’une Ellipse allongée vers les Poles, dont la propriété est telle, qu’étant divisée en degrés, par des perpendiculaires élevées sur sa surface, chacun de ces degrés diminüe en s’approchant des Poles, & augmente en s’écartant.
[Cassini II, p. 238]
Dans les discussions qui s’ensuivent, les zones géographiques mesurées sont jugées trop restreintes pour fournir des indications pertinentes. Une expédition est organisée pour mesurer un arc de méridien au nord du Pérou, au voisinage de l’équateur. Godin, La Condamine, Bouguer, Joseph Jussieu embarquent en mai 1735. Mais l’impatience est grande chez certains des protagonistes. Pierre-Louis Maupertuis (1698-1759), newtonien convaincu, obtient l’organisation d’une deuxième expédition au voisinage du cercle polaire, il quitte la France en avril 1736, en compagnie notamment d’Alexis Clairaut (1713-1765). Le voyage n’est certes pas de tout repos, mais sur place les savants bénéficient d’un soutien des autorités suédoises, ils sont de retour à Paris en Aout 1737 tandis que l’équipe du Pérou reste enlisée dans les difficultés matérielles et les dissensions. Maupertuis triomphe, ses mesures confirment la thèse newtonienne : à une latitude de 66°, le degré de méridien mesure 57438 toises. Dans ses extrapolations, Cassini II ne prévoyait que 56 508 toises à cette latitude. [Cassini II, p. 245]
| Cassini II : Entre Paris et Collioure Entre Paris et Dunkerque | 57097 toises 56 960 toises |
| Extrapolation par Cassini pour un degré à la latitude 66° | 56508 toises |
| Mesure de Maupertuis à la latitude 66° | 57438 toises |
La méridienne vérifiée par Jacques et César-François Cassini
En 1733, Cassini II se voit à nouveau confier la tâche de cartographier le royaume. Il saisit là l’occasion de reprendre la mesure du méridien de Paris. Son fils, César-François (1714-1785, dit Cassini III) participe aux travaux et en donne un compte rendu détaillé en 1744. Par rapport aux premières campagnes de mesure, les instruments ont été améliorés par l’utilisation d’un micromètre. On a pu gagner en précision tout en réduisant un peu le rayon des quarts de cercle devenus plus maniables.
Les triangles de la partie septentrionale
Six bases sont mesurées de nouveau. Le tronçon séparant les deux bases septentrionales s’étend de Villers-Bretonneux (près d’Amiens) jusqu’à Dunkerque. Une première suite de triangles est utilisée.
La distance entre le parallèle d’Amiens et celui de Dunkerque est évaluée en projetant 5 des côtés sur le méridien. Une seconde évaluation est faite à partir d’une nouvelle série de mesures comportant deux triangles différents. C’est la moyenne des deux résultats qui a été retenue. Une vérification est opérée par une troisième chaîne mais, elle n’est pas utilisée parce que moins fiable : pour certains triangles l’un des angles a été déduit des deux autres sans être directement mesuré [p. 59].
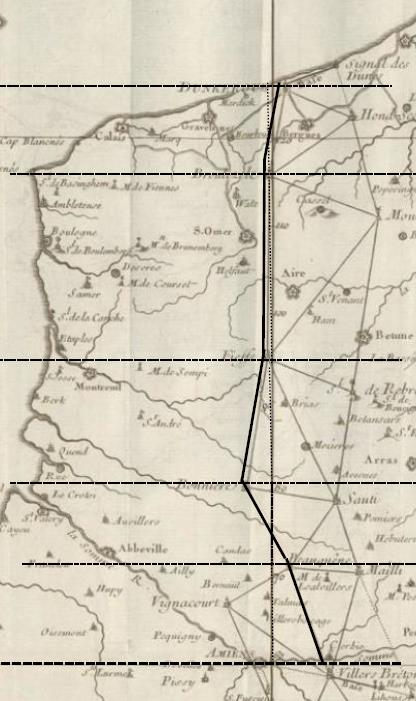
fig. 19
A l’extrémité nord, on a cherché à utiliser la même base que les prédécesseurs. Le repère utilisé dans les dunes a évidemment disparu. Un nouveau signal est érigé. Le rapport précise que le trajet entre ce signal D et le Fort du Revers R rencontre l’obstacle d’un canal (C). On a donc mesuré avec les perches la distance DA en s’arrêtant avant le canal, puis on a cheminé perpendiculairement à DA jusqu’au point P tel que l’angle RPA soit égal à 45°(fig. 19). On a obtenu ainsi une mesure de DA+AP égale à la distance cherchée DR.
fig. 20
Aujourd’hui, des retours sur trois siècles d’histoire locale sont parfois nécessaires si l’on veut évoquer les traces des différentes stations utilisées par les Cassini. A Dunkerque, le Fort du Revers, déjà en ruines au XVIIIème siècle, a complètement disparu ; sur le port, une Rue du Revers en perpétue le souvenir ; par contre la Tour du Leughenaer est toujours debout. A Hondschoote et à Bollezeele (nommé alors Broulezele), les clochers des églises sont toujours là. Au sommet du Mont des Cats (nommé alors Mont des Chats), le moulin qui a servi de repère a été détruit pendant la guerre 14-18. De nombreuses mesures annexes ont concerné des lieux utiles à la cartographie mais qui n’interviennent pas nécessairement dans la mesure du méridien (voir [Cassini III 1744, p. 166 -202]). Par exemple, à Bergues, il est question de l’abbaye Saint Winoc, laquelle a été rasée après la Révolution, mais ses tours ont été préservées parce qu’elles servaient de repère pour la navigation. A Lille il existe encore une église Saint Sauveur, elle a été construite vers 1900 à l’emplacement de celle qui est mentionnée par les Cassini, celle-ci avait perdu la flèche de son clocher pendant le siège de Lille par les Autrichiens en 1792, puis l’église toute entière avait été détruite par un incendie en 1898. A Arras, la cathédrale Saint Vaast et sa flèche ont été détruites pendant la Révolution. Non loin de là, les tours de l’abbaye de Mont Saint Eloi sont en ruine, elles restent néanmoins présentes dans le paysage…
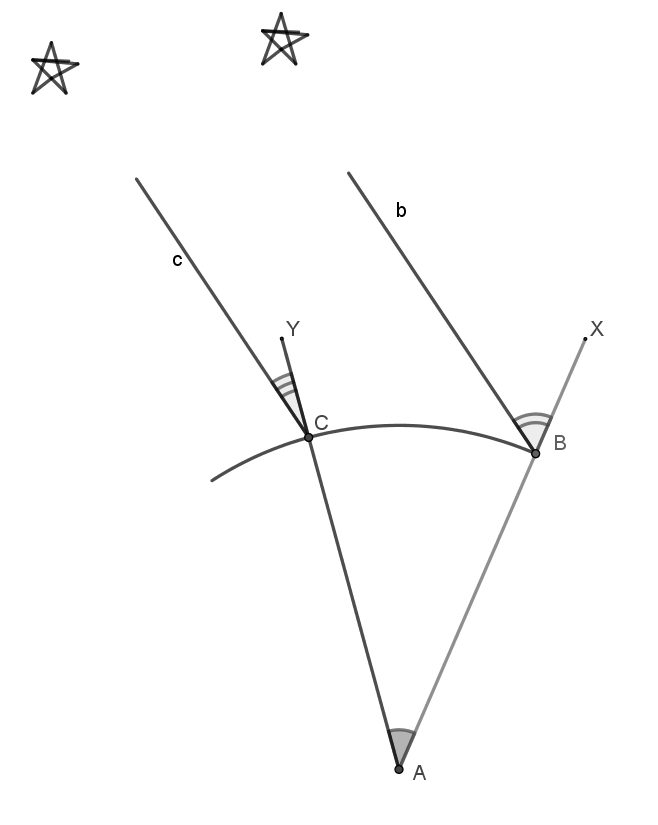
Des angles corrigés
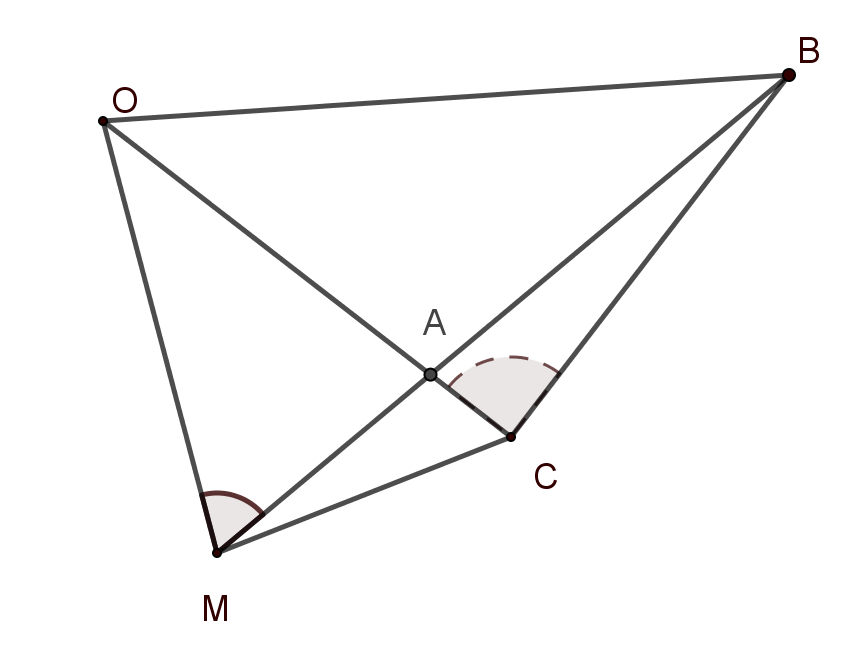
Le cas échéant, la mesure des angles peut faire l’objet d’une correction nommée « réduction au centre ». Le principe en est donné à propos du triangle BOM dont les sommets sont constitués par le clocher de Brie, l’Observatoire de Paris et la tour de Montlhéry [Cassini III 1744, p. vi] (fig. 21). Cette dernière tour a été observée depuis les points O et B ; mais les difficultés matérielles n’ont pas permis d’installer le quart de cercle au sommet de la tour pour évaluer l’angle OMB, on a dû effectuer les visées depuis un point voisin C et on a donc mesuré l’angle OCB. L’angle OAB est extérieur au triangle OAM, on peut donc écrire :
Mais le même angle OAB est aussi un angle extérieur du triangle ABC, il peut donc s’évaluer à partir des angles en B et en C de ce triangle, d’où :
Les angles MBC et MOC peuvent s’obtenir en résolvant les triangles OMC et BMC (il suffit d’un calcul approché utilisant une première approximation des distances MB et MO).
Tous les angles utilisés ont été effectivement mesurés (aucun n’a été simplement déduit des valeurs trouvées pour les deux autres angles du triangle). Quand la somme des trois angles obtenus n’est pas égale à 180°, on corrige cette « erreur de fermeture » en appliquant une règle systématique :
On a réparti sur chacun des angles qui forment les triangles, à proportion de sa grandeur, la différence qui se trouvoit entre leurs sommes et 180°. Ces angles, ainsi corrigés, forment les triangles que nous employons dans le calcul.
[Cassini III 1744, p. 26]
Chacun des triangles mesurés est considéré comme un triangle dessiné dans un plan tangent à la surface de la terre. Dans les régions de plaines, on peut considérer que les stations A, B, C qui matérialisent un tel triangle sont de même niveau et appartiennent à un même plan tangent à la sphère terrestre et ainsi les stations B et C sont vues du point A dans le plan de l’horizon. Mais ailleurs, le relief peut obliger à effectuer une « réduction à l’horizon ». Les corrections à opérer sont étudiées dans un mémoire publié par Cassini III en 1739 (en particulier p. 70). Les différents cas de figure sont examinés : l’une des stations visées est dans le plan de l’horizon et l’autre au-dessus de ce plan, les deux stations sont au-dessus de l’horizon, l’une est au-dessus, l’autre au-dessous … On peut donner les principes de cette réduction dans les termes suivants.
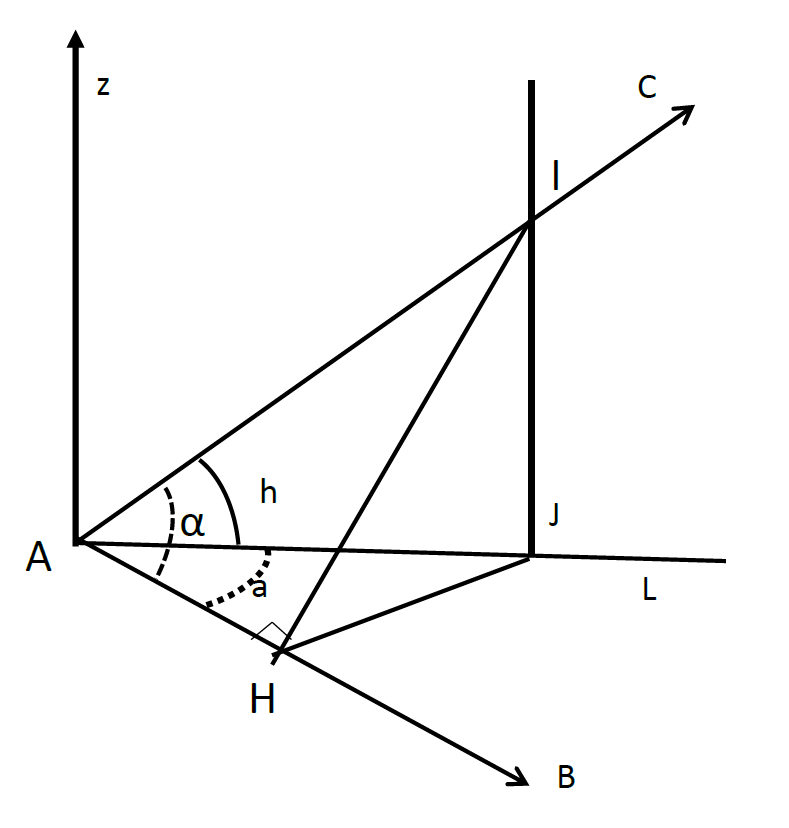
Supposons que la station B soit vue de A dans le plan de l’horizon, mais que la station C occupe une position plus élevée (fig. 22). Le plan vertical contenant AC rencontre le plan horizontal suivant la droite AL, et l’élévation de C est mesurée par l’angle CAL = h. L’angle observé est BAC = α. Il s’agit d’évaluer l’angle « réduit à l’horizon » BAL = a. Un point I de la droite AC se projette orthogonalement en J sur AL et en H sur AB, on démontre alors facilement la relation
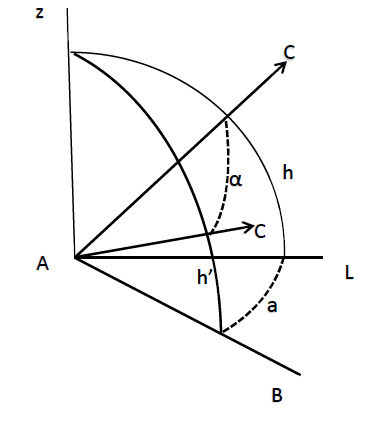
Si les deux stations B et C sont plus élevées que A (fig. 23), l’angle réduit à l’horizon se calcule au moyen d’une formule de trigonométrie sphérique
Retour sur la figure de la Terre
Le mémoire de Cassini III évalue la longueur d’un degré de méridien en divers lieux dont les latitudes variant de 43° à 49°. Il constate que la longueur du degré augmente lorsque la latitude augmente, il mentionne une seule exception dans le passage du sud au nord de la ville de Rodez, mais il admet :
la différence est trop légère pour être attribuée à autre chose qu’aux erreurs inévitables dans des observations qui demandent une subtilité & des attentions extraordinaires. Un accord trop parfait dans ces sortes d’opérations ne serviroit qu’à les rendre suspectes à ceux qui ont quelque expérience dans la pratique de la Géométrie & de l’Astronomie
[Cassini III 1744, p. 112-113]
Il en conclut que la terre est aplatie vers les pôles.
Géométrie, analyse, théorie des probabilités
Une nouvelle mesure du méridien est entreprise après la Révolution, dans le but explicite de fonder le système métrique. Les travaux sont effectués de 1792 à 1799 par Jean-Baptiste Delambre (1749–1822) et Pierre Méchain (1744–1804).
La précision des mesures est améliorée par le recours au « cercle répétiteur » ; par exemple, s’il s’agit d’évaluer un angle α, des rotations successives de la lunette vont d’abord permettre de lire sur le limbe la valeur de 10 α, l’incertitude sur la mesure de α est donc a priori divisée par 10. En réalité, les angles observés ont toujours été les angles d’un triangle sphérique ABC (fig. 24). La petite taille des triangles et la précision des mesures initiales autorisaient à les considérer comme des triangles plans (pour des triangles « grands » on peut voir en annexe les difficultés que l’on rencontre pour les représenter dans le plan) . Mais on sait que la somme des angles d’un triangle sphérique est supérieure à un angle plat, l’excès sphérique ε (différence entre cette somme et un angle plat) est proportionnel à la surface du triangle
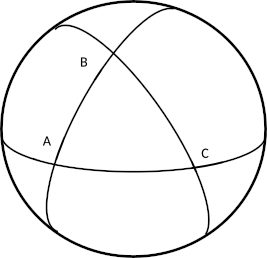
Dès 1787, André-Marie Legendre (1752-1833) s’est posé la question de la réduction à opérer sur ces angles pour pouvoir considérer le triangle ABC comme un triangle plan. En utilisant les développements en série des fonctions sinus et en considérant que le triangle est suffisamment petit, il a démontré que l’on peut considérer ABC comme un triangle plan et lui appliquer la loi des sinus à condition de substituer aux angles , , les angles
, [Delambre 1799, p. 13]. On dispose alors d’un point de vue et d’un procédé nouveau pour corriger ce qui était alors classé dans la rubrique de « l’erreur de fermeture ».
Plus généralement, après les travaux des Cassini, les méthodes de calcul ont évolué, comme en témoigne l’ouvrage publié par Delambre en 1799, Méthodes analytiques pour la détermination d’un arc de méridien. La recherche de formules générales permet de simplifier et de systématiser les opérations ; par exemple, en ce qui concerne la réduction au centre, Delambre souligne qu’il a résumé en une seule formule les onze cas examinés successivement dans la Méridienne corrigée de Cassini III [Delambre 1798, p. vii]. Après les simples considérations de géométrie élémentaire, l’analyse (en particulier avec les développements en série) accroît l’efficacité et la précision des travaux géodésiques.
Mais au début du XIXème siècle, une autre évolution se profile, elle concerne la façon de prendre en compte l’incertitude avec laquelle les mesures sont réalisées. Par exemple, quand on a calculé les triangles d’une chaîne à partir d’une première base, et que l’on mesure une seconde base à l’autre extrémité, on modifiait les résultats de façon empirique pour tenter de les rendre cohérents avec les deux bases mesurées. Ce type de problème sera traité ultérieurement par une Théorie des erreurs reposant sur la loi de Gauss-Laplace et sur la méthode des moindres carrés. Les pratiques de calcul qui en découlent seront d’abord le fait des géodésiens allemands. Il faudra attendre la deuxième moitié du XIXème siècle pour que les géodésiens français prennent conscience du retard accumulé en ce domaine. (voir à ce sujet [Jozeau, 1997]).
BIBLIOGRAPHIE
Sources primaires
AL BIRUNI
[1967] The Determination of the Coordinates of Positions of Distances between Cities, traduction par Jamil Ali du Kitāb taḥdīd nihāyāt al-amākin li-taṣḥīḥ masāfāt al-masākin (1025), Beyrouth : American University, 1967.
BOUGUER Pierre
[1749] La figure de la terre, déterminée par les observations de messieurs Bouguer, & de La Condamine, Paris : Jombert, 1749
CASSINI II Jacques
[1720] De la grandeur et de la figure de la terre, suite des Mémoires de l’Académie des Sciences, année 1718, Paris :1720.
CASSINI III César-François (dit Cassini de Thury)
[1739] Des opérations géométriques que l’on employées pour déterminer les distances sur terre et des précautions qu’il faut prendre pour les faire le plus exactement qu’il est possible, Mémoires de l’Académie Royale des Sciences (1736), p. 64-86.
[1744] La Méridienne De L’Observatoire Royal De Paris, Vérifiée dans toute l’étendue du Royaume par de nouvelles Observations, A Paris, chez Pierre-Charles, Guérin…
DE LALANDE Joseph
[1789] Sur la mesure de la Terre que Fernel publia en 1528, Mémoires de l’académie royale des sciences (1787), Paris, 1789, p. 216-222
DELAMBRE, Jean B.
[1798] Méthodes analytiques pour la détermination d’un arc du méridien : précédés d’un mémoire sur le même sujet. Paris : Duprat, an VII [1798/99]
[1806, 1807, 1810] Base du système métrique décimal ou mesure de l’arc du méridien compris entre les parallèles de Dunkerque et de Barcelone. Tomes 1, 2, 3, Paris, 1806, 1807, 1810
PICARD Jean-Félix
[1671] Mesure de la Terre, Paris, Imprimerie royale, 1671
PICARD Jean-Félix et La HIRE
[1719] Observations faites aux Côtes septentrionales de France en 1681. Par MM Picard et De La Hire, Mémoires de l’Académie Royale des Sciences pour l’année 1718, tome VII partie I, p. 399-413.
Sur la géodésie et la cartographie
GHYS Etienne
[2010] Représenter les mondes
JOZEAU Marie-Françoise
[1997] Géodésie au XIXème siècle : de l’hégémonie française à l’hégémonie allemande. Regards belges. Thèse de l’université Diderot Paris VII, 1997
LACOMBE Henri, COSTABEL Pierre (sous la direction de)
[1988] La figure de la terre du XVIIIe siècle à l’ère spatiale, actes du Colloque national organisé par l’Académie des Sciences, janvier 1986, Paris : Gauthier-Villars, 1988.
LEFORT Jean
[2004] L’aventure cartographique, Paris : Belin, 2004
LEVALLOIS Jean-Jacques (sous la direction de)
[1988] Mesurer la Terre, 300 ans de géodésie française, de la toise du Chatelet au satellite, Paris : bibliothèque de l’Association Française de Topographie, 1988
PELLETIER, Monique.
[1990] La carte de Cassini : l’extraordinaire aventure de la carte de France, Presses de l’Ecole nationale des ponts et chaussées. Paris – 1990
TAZZIOLI Rossana
[2008] Gauss, prince des mathématiciens, Les génies de la science, pour la Science n° 36, août-sept. 2008.
[2013] La mesure de la terre et la théorie des surfaces
Dans les classes
HENNEQUIN Paul-Louis
[2007] Mesurer la Terre avec des élèves, bulletin de l’APM, n° 410, p. 300-310
IREM de Clermont Ferrand
Travail interdisciplinaire sur Cassini
IREM Paris VII
[1996a] Approche de la cartographie, Mnémosyne n°11, Février 1996
[1996b] Méthode mathématique de représentation de la terre, Mnémosyne n°12, Juin 1996
QUINTON Pascal
[2002] Activités mathématiques à propos de la mesure de la Terre, Repère-Irem n° 49, oct. 2002, p. 73-92
Récits historiques, fictions
ARAGO François
[1854] Histoire de ma jeunesse / François Arago : préf. de Jean-Christophe Bailly ; introd. par Alexandre de Humboldt. Réédition Paris : Ch. Bourgois
GUEDJ Denis
[2000] Le mètre du monde, Le Seuil-Points, 2000
SIMAAN Arkan
[2001] La science au péril de sa vie : les aventuriers de la mesure du monde ; Paris : Vuibert : ADAPT, 2001.
TRYSTRAM Florence
[1993] Le procès des étoiles – le récit de la prestigieuse expédition de l’Académie des sciences en Amérique du Sud, 1735-1771, Payot, 1993.
VERNE Jules
[1872] Aventures de trois Russes et de trois Anglais dans l’Afrique Australe, Paris : Hetzel.
ANNEXE
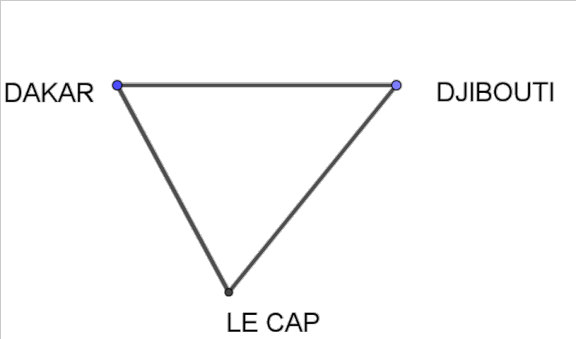
Une activité (inspirée de [Ghys]) permet d’introduire le problème de la représentation plane des éléments du globe terrestre. Le tableau ci-dessus donne les distances relatives (mesurées à la surface du globe) des quatre villes Rome, Dakar, Djibouti, le Cap.
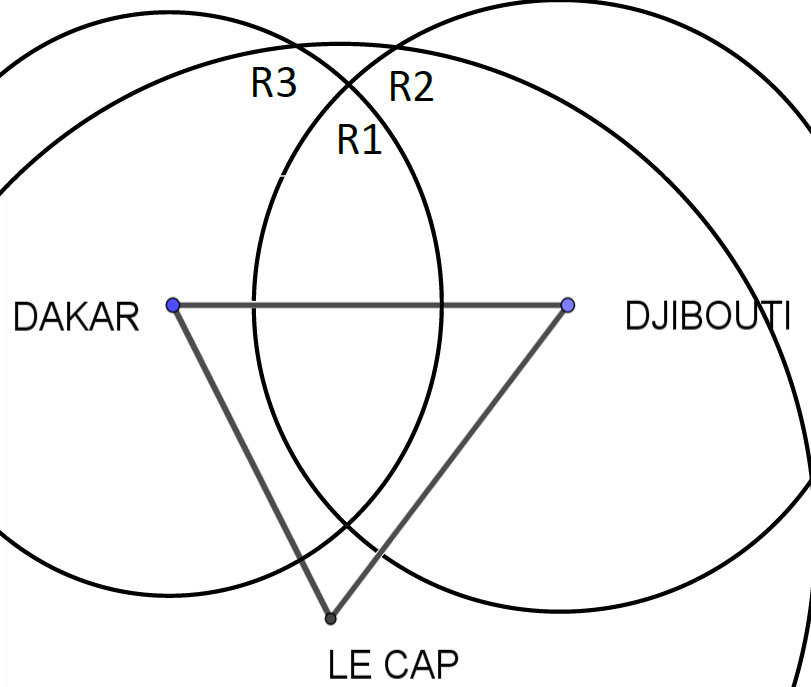
On fournit aux élèves une feuille où le triangle Dakar-Djibouti-Le Cap (fig. 26) a été représenté en utilisant les distances (en gras du tableau ci-dessus) avec une échelle donnée. Puis on demande de placer sur ce schéma le point R représentant la ville de Rome. On s’aperçoit qu’il est impossible de trouver, dans le plan un point qui permette de respecter les distances aux trois villes de Djibouti, Dakar, Le Cap (fig 27).
| DJIBOUTI | DAKAR | LE CAP | |
| ROME | 4437 | 4170 | 8453 |
| DJIBOUTI | 5956 | 5693 | |
| DAKAR | 5028 |