Auteur : Sébastien Dumoulard
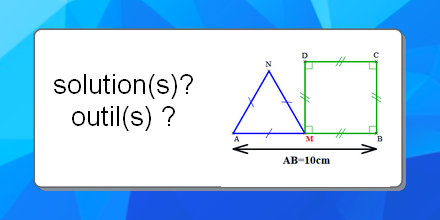
Résoudre un problème de périmètre :
•obtention d’un encadrement à l’unité de la solution par le calcul mental ;
•obtention d’un encadrement au dixième de la solution à l’aide d’un logiciel de géométrie dynamique (ici TracenPoche) ;
•obtention d’ encadrement(s) plus fin(s) de la solution à l’aide du tableur ;
•résolution exacte par l’algèbre.
Déroulement
- Lieux : salle pupitre puis classe.
- Durée : 1 heure 30 minutes (1 h en classe informatique, puis 30 minutes de synthèse en classe, à l’aide d’un vidéo projecteur).
- Matériel élève :
- un poste informatique par élève
- traitement de texte
- tableur
- logiciel de géométrie dynamique (ici Tracenpoche)
- Matériel professeur : un vidéo projecteur pour la synthèse en classe.
Buts
- Résolution approchée d’un problème avec plusieurs outils (géométrie dynamique, tableur) puis résolution exacte de façon algébrique.
Prérequis
- Savoirs : notion de périmètre, notion de base du calcul littéral.
- Savoir-faire : résoudre une équation du 1er degré à une inconnue.
Commentaire
Activité utilisant TracenPoche ou GeoGebra, à adapter pour d’autres logiciels de géométrie dynamique, tels Cabri-Géomètre, Géoplan, et/ou à approfondir dans un autre niveau du collège (3e avec l’étude graphique des fonctions affines par exemple, voir les fichiers TracenPoche et GeoGebra joints à l’article).
Documents
Transfert par E.O.
