Cet article a été publié pour la première fois dans l’ouvrage :

Mathématiques en perspectives : hommage à Rudolf Bkouche,
dir. G. Jouve, A.-M. Marmier, M. Moyon, F. Recher, R. Tazzioli, D. Tournès
Limoges : PULIM, 2020

La version ci-dessous est une présentation adaptée au web enrichie de figures interactives de l’atlas EMTA.
En complément à cet article, on peut lire aussi l’article De la géométrie élémentaire dans les travaux géodésiques.

---

Dans cette contribution, nous proposons une introduction à la géométrie du cadastre telle qu’elle a pu être pratiquée au début du XIXe siècle. Lors des journées en l’honneur de Rudolf Bkouche, l’atelier que nous avons proposé consistait à lever le plan de polygones quelconques tracés sur le sol, avant de comparer les méthodes intuitivement proposées aux procédures ayant effectivement été utilisées par les géomètres du cadastre.

Il ne saurait ici être question de reproduire à l’identique cette activité. Il nous a semblé plus intéressant de proposer, à l’attention des étudiants, enseignants et formateurs curieux, une introduction à la fois ramassée et précise pour s’approprier l’outil que représente le cadastre. Notre intuition centrale est la conviction que l’approche historique du cadastre napoléonien est un outil prometteur pour l’enseignement de la géométrie en lien avec d’autres disciplines, notamment l’histoire et la géographie.

Développée au cours d’enseignements en formation des maîtres, cette réflexion sur la géométrie repose sur deux principes essentiels. Le premier est celui de l’utilisation de l’histoire des mathématiques et de leur enseignement : au XIXe siècle, on a effectivement enseigné la géométrie de l’arpentage avec des méthodes élémentaires, ce qui constitue une ressource précieuse pour l’enseignement actuel. Second principe, cette géométrie possède un sens et des objectifs évidents pour celui qui réalise la tâche, tout en laissant une latitude considérable quant au choix des méthodes et des instruments. C’est une géométrie du quelconque, essentiellement pratique, qui suppose une vraie réflexion sur les polygones.

Nous proposons donc ici certains outils et références qui ont vocation à être utilisés ailleurs. Le levé de plan combine la généralité des méthodes de la géométrie élémentaire et la spécificité des contextes, des techniques et des lieux. En partant de sa culture mathématique propre, tout enseignant ou étudiant est rapidement en mesure d’analyser le cadastre de sa région ou de sa commune, apportant ses connaissances locales pour mieux comprendre son environnement, afin d’en faire bénéficier ses collègues et élèves. L’activité fondamentale de la géométrie de l’arpentage est le levé de plan. La réalisation du cadastre napoléonien dans la première moitié du XIXe siècle a ainsi consisté à lever le plan de dizaines de milliers de communes. Il s’agit d’une tâche scientifique, consistante et authentique. Enseignée dans une myriade de manuels de l’époque, elle repose sur les mathématiques élémentaires aujourd’hui enseignées dans les cycles 3 et 4 [note 1].

---

La géométrie du cadastre napoléonien

Il est possible d’approcher cette géométrie du cadastre en étudiant les manuels de géométrie élémentaire de cette époque. Il en existe une grande variété, souvent numérisés et disponibles au téléchargement – une ressource précieuse pour l’enseignant de mathématiques. Nous nous servirons ici d’un Manuel d’arpentage pour les écoles primaires [note 2] rédigé à la fin du XIXe siècle par « une réunion de professeurs » [note 3].

Une question centrale de ces manuels, qui correspond à l’activité proposée dans notre atelier, est de « tracer en petit sur le papier la figure exacte d’un terrain avec tous ses détails, en conservant l’égalité des angles et la proportionnalité des côtés [note 4] ». Sont alors présentés les outils nécessaires : la chaîne d’arpenteur, un décamètre en métal formé de chaînons de 20 centimètres, ainsi que l’équerre d’arpenteur (dont nous ne parlerons pas ici, mais qui possède un grand intérêt pour l’enseignement), la planchette, le graphomètre et la boussole.

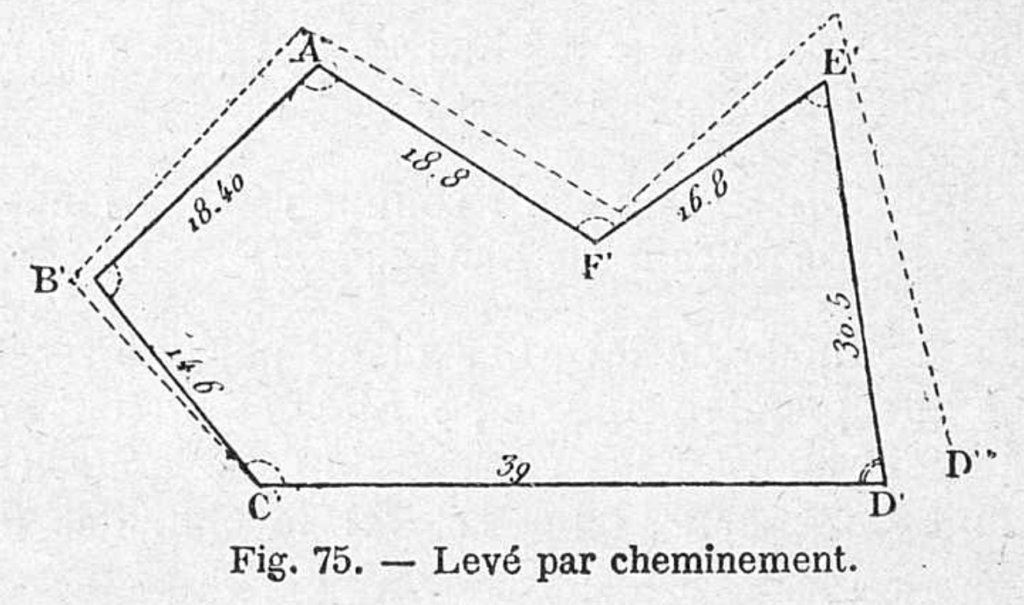
Chaque manuel présente plusieurs méthodes, parmi lesquelles nous exposerons ici la méthode par rayonnement, la méthode par intersection et la méthode par cheminement. La méthode par cheminement est celle qui est la plus spontanément mobilisée pour lever un plan (Fig. 1).

Partant d’un premier segment [D’C’], on mesure ou reporte sur le papier l’angle D’C’B’, puis on mesure la distance B’C’ à laquelle on applique un coefficient de réduction pour mettre à l’échelle. On mesure ensuite l’angle C’B’A’, et on chemine ainsi autour du polygone. La vérification de la figure est rapide : il suffit de mesurer le dernier angle sur le papier et de comparer avec le terrain. Dans les faits, cette méthode se révèle souvent imprécise, puisque les erreurs de mesures tendent à se cumuler, comme le tracé en pointillé (Fig. 1) le suggère élégamment. C’est cependant parfois la solution la plus simple, par exemple s’il faut lever le plan d’un bois impénétrable.

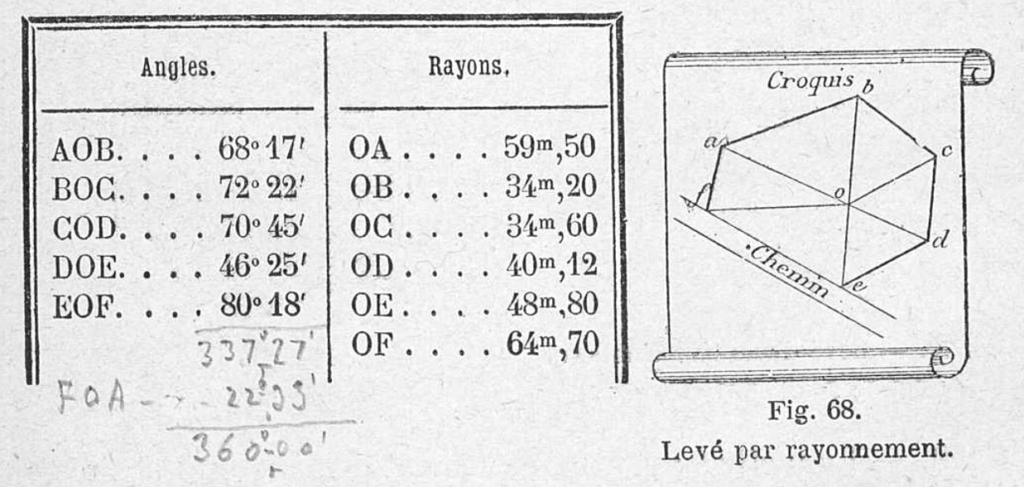
Quand c’est possible, les géomètres tendent à lui substituer la méthode par rayonnement (Fig. 2). On commence par localiser un point central O, duquel on peut viser plusieurs points remarquables. On doit ensuite mesurer l’ensemble des angles AOB et BOC, etc., et immédiatement vérifier si leur somme est égale à 360°. La mesure des distances des divers points au point central, ici nommées « rayons » permet ensuite de lever le plan. Cette méthode est plus efficace, d’une part car l’ensemble des angles sont levés depuis le centre, et d’autre part car il est possible de rajouter de nombreuses mesures de vérification à l’intérieur de chaque triangle considéré.

Comme nous le verrons ci-dessous, la méthode par rayonnement constitue le cas d’école que cherche à obtenir le géomètre-arpenteur. Si la configuration ne s’y prête pas, il est possible d’utiliser la méthode par intersection (Fig. 3).

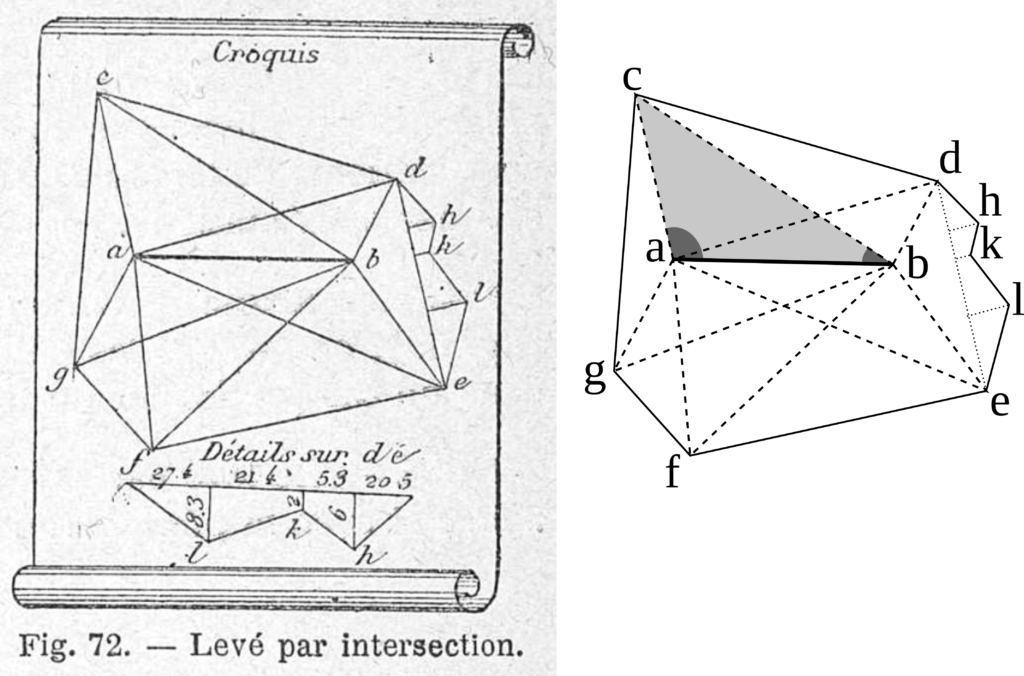
Cette méthode consiste à « joindre deux stations à tous les sommets du périmètre à lever, à mesurer la longueur de la droite ou base, qui réunit les deux stations, et les angles que chaque ligne amenée forme avec la base [note 5] ». Plus simplement, on peut directement tracer les angles sur le plan et en déduire les données recherchées. Dans (Fig. 3), en partant de la base [AB], on vise le point C successivement depuis A et B en reportant les angles sur le plan. Il devient ainsi possible de connaître toutes les longueurs voulues, en ayant recours à l’échelle du plan.

La théorie de l’arpentage exposée ici est une simplification assez grossière, limitée au levé d’un polygone quelconque. Comme le montre dans (Fig. 3) le cas de la portion EDHKL, une méthode doit souvent être accommodée pour tenir compte de difficultés ponctuelles.

Cette brève présentation permet cependant de faire ressortir des points communs aux diverses méthodes. Dans tous les cas, on utilise des propriétés géométriques élémentaires, souvent de manière implicite et très efficace. Le levé de plan repose sur l’utilisation des triangles semblables et accorde donc un rôle important à la proportionnalité et aux échelles. On combine souvent les relevés d’angles et de longueurs, mais les relevés de grandeurs ne passent pas forcément par la mesure : dans la méthode par cheminement, les angles sont seulement reportés, tandis que la méthode par intersection permet d’obtenir des segments à l’échelle sans les avoir mesurés.

À partir de ces bribes de géométrie pratique, nous voulons montrer qu’il est possible de réaliser une exploitation tout à fait intéressante des cadastres locaux. Il est pour cela nécessaire de faire interagir les mathématiques et l’histoire ainsi que la géographie locale, mais toutes les connaissances mises en jeu sont abordables dans un cadre scolaire sans simplification excessive.

---

Explorations dans le cadastre napoléonien

Pour comprendre l’étude du cadastre, un détour par l’histoire s’impose. Avant la Révolution française, les diverses tentatives de proposer un cadastre général de la France n’ont pas abouti. La nécessité de réformer la fiscalité rend nécessaire l’établissement d’un cadastre, dont les modalités concrètes ne seront finalement adoptées qu’en 1807, d’où son nom de cadastre napoléonien [note 6].

Ce cadastre, pour la plupart des départements, est accessible en ligne. Quelles planches explorer ? Celles de notre commune par exemple. L’atelier s’est déroulé au bâtiment M1 du campus scientifique à Villeneuve-d’Ascq dans le Nord (banlieue de Lille), commune récente qui est le fruit d’une fusion entre plusieurs communes dont celle d’Annappes [note 7].

Sur le terrain, les opérations cadastrales sont confiées à des bataillons de géomètres de première ou seconde classe, délimitateurs ou vérificateurs. Dans notre exemple, celui de la commune d’Annappes, le cartouche du cadastre de 1816 indique que le géomètre du cadastre était Mr. Barbotin, tandis que l’ingénieur-vérificateur était Mr. Robin. Deux questions, aussi simples que fondamentales, peuvent alors être posées : quelle formation mathématique possédait Barbotin ? Quelles méthodes géométriques utilisait-il pour lever le plan d’une commune ?

La formation des géomètres du cadastre était élémentaire ; il est pourtant difficile de se mettre spontanément à leur place pour lever un plan. La géométrie scolaire actuelle étudie principalement des configurations spécifiques comme la classification des triangles et quadrilatères. La géométrie du cadastre est une géométrie du quelconque, le polygone n’ayant a priori pas de propriétés spécifiques. On sait cette géométrie de terrain évidente et pourtant elle nous déconcerte : c’est précisément ce décalage qui présente un intérêt historique et didactique.

La formation de Philogone Barbotin illustre la dynamique du cadastre au début du XIXe siècle. Probablement né aux environs de Douai [note 8], il est âgé de 18 ans lorsqu’il s’inscrit, en 1804, à l’école de géométrie de Douai. Cette école, modelée sur son équivalent parisien, a comme unique but de former des géomètres du cadastre. Le citoyen Raux, par ailleurs enseignant à l’école d’artillerie, y propose des cours de géométrie et d’arithmétique élémentaire [note 9] . Après sa formation, Barbotin sera affecté à Lille en 1806 et y restera pendant de nombreuses années. Le cadastre d’Annappes, qu’il réalise en 1816, n’est qu’une de ses nombreuses productions, que l’on peut supposer soignées puisqu’il sera nommé en 1817 géomètre-délimitateur [note 10].

Étudions maintenant en détail le cadastre. Les archives du Nord ont mis en ligne le tableau d’assemblage (Fig. 5) permettant de situer les planches de l’atlas indiquant le découpage parcellaire. Cet atlas est constitué des trois sections A, B et C de deux feuilles chacune. Étant avant tout un outil du ministère des finances permettant la levée des impôts fonciers, le cadastre parcellaire comprend aussi un tableau indicatif et une matrice cadastrale. Le tableau indicatif est le cahier renseignant pour chaque numéro de parcelle, le nom du propriétaire, la nature et la contenance du terrain. Les parcelles 661 et 662 de la section C2 sur lesquelles est implanté le bâtiment M1 appartenaient au baron de Brigode (Fig. 6). À l’aide du numéro de folio, on peut retrouver dans le cahier appelé matrice cadastrale la liste des parcelles par propriétaire. Le numéro de folio du baron de Brigode est le 169, la matrice cadastrale est en trop mauvais état pour être consultée.

Les premières opérations du géomètre sont la délimitation et le bornage de la commune. Vient ensuite le canevas trigonométrique qui est inscrit sur le tableau d’assemblage (Fig. 5). C’est une étape importante dans la conception du cadastre puisqu’il s’agit de trianguler la commune à l’aide d’un certain nombre de repères fiables notés sur le plan par des lettres. Dans la pratique, cette opération n’était pas toujours estimée comme nécessaire par les géomètres. Le ministère note dès 1807 que certains géomètres ne réalisaient ce canevas qu’une fois l’arpentage terminé. Il rappelle ainsi l’intérêt d’un tel canevas :

En effet, les points trigonométriques peuvent être considérés comme des fils que saisit constamment le Géomètre pour ne pas s’égarer dans le labyrinthe des détails. Si ces points n’existent pas, sa marche, qui ne peut être exacte qu’autant qu’elle est constante et directe, devient incertaine et sinueuse [note 11].

Si le travail de triangulation réalisé par le géomètre Barbotin pour la commune d’Annappes en 1816 semble être réalisé sérieusement, nous pouvons soupçonner ce même Barbotin d’avoir négligé en 1825 cette tache pour Ascq, une commune voisine : les traits au crayon que l’on trouve sur la section B1 montrent de nombreuses imprécisions et hésitations pour un canevas qui ne sera finalement pas celui retenu pour le tableau d’assemblage. De manière plus générale, si des directives ministérielles tentent d’imposer une pratique normative, on constate une grande variété de pratiques locales qui font que chaque planche de cadastre est singulière, bien que respectant un certain nombre de règles édictées.

Pour le cadastre d’Annappes, quels sont ces « fils que saisit constamment le Géomètre pour ne pas s’égarer dans le labyrinthe des détails » ? Quel est le travail géométrique qui sous-tend ce cadastre ? Pour la suite de l’exposé, le lecteur est invité à consulter les figures 5 et 6, ou pour plus de confort retrouver les planches du cadastre en ligne [note 12].

Sur le tableau d’assemblage, on identifie la méridienne du chef-lieu (passant par le clocher de l’église noté C) et sa perpendiculaire. La rose des vents est opportunément placée sur la perpendiculaire. D’autre part, deux points A et B sont choisis pour constituer une base dont la longueur est mesurée très soigneusement à la chaîne d’arpenteur (1478 mètres) (Fig. 7). Ces points doivent être suffisamment éloignés, visibles l’un de l’autre et joignables sans obstacles. Barbotin choisit deux points de la plaine située au sud de la commune. Le point A est stratégique : dans l’alignement de deux clochers (C et F ), facilement accessible (sur le bord d’une route) et repérable de loin (près d’un moulin). La base sert de référence à l’ensemble du canevas. Idéalement, on devrait pouvoir voir tout autre point de la commune des points A et B et la « méthode par intersections » citée plus haut permettrait de lever tous les points du terrain. La vue dégagée du point A permet déjà au géomètre de viser des points éloignés : clochers des communes voisines (E et F ), un moulin (G), des signaux probablement artificiels (couples de points alignés à A : K et N , L et M , B et R). Le polygone BCDEFGHKL centré sur le point A peut ainsi être construit de manière très précise : maîtrise des angles au centre, du rayon AB et des angles du cheminement le long des côtés du polygone. On retrouve ici l’intérêt de la « méthode par rayonnement » étudiée plus haut. Le clocher de l’église était probablement accessible au géomètre [note 13]. De ce point C, il pouvait viser A, B, T , V , W , D pour construire de manière robuste un nouveau polygone [note 14] (Fig. 8).

La difficulté pour Barbotin a été d’associer la partie nord de la commune à la base [AB]. C’est le point R sur le prolongement de cette base [AB] qui permet de créer un lien direct. Il permet de viser un point V situé sur la route longeant le nord du château du baron de Brigode (section B1). Le long de cette route, Barbotin bénéficie d’une autre heureuse percée entre le parc arboré du château et le bois voisin pour pouvoir établir un point U visible de la partie sud de la commune. [U V ] peut devenir une base secondaire relativement fiable permettant au géomètre de prolonger le canevas dans la partie nord d’Annappes (Fig. 9). On remarque, à la taille des triangles, que la progression se fait dans un paysage beaucoup plus hostile : marais, reliefs, habitations, zones boisées. Même le point X, qui est pourtant un moulin, est difficilement visible. Barbotin a néanmoins réussi à construire un canevas de 42 points dont chaque point appartient à au moins deux triangles (à l’exception des points L0 , S 0 et R0 ). Toute incohérence sur la construction d’un triangle pouvait donc être décelée grâce à la construction d’un triangle adjacent.

Ce canevas ayant été fait très soigneusement, Barbotin a pu ensuite entrer dans les détails du tracé des parcelles en se référant constamment aux « fils » qu’il a tendus. Les sections de l’atlas rendent ainsi compte de ce pavage en polygones quelconques que sont les parcelles. L’étape finale du levé de plan à l’échelle des terres, maisons et rues se fait avec les mêmes méthodes que précédemment (cheminement, intersection, rayonnement).

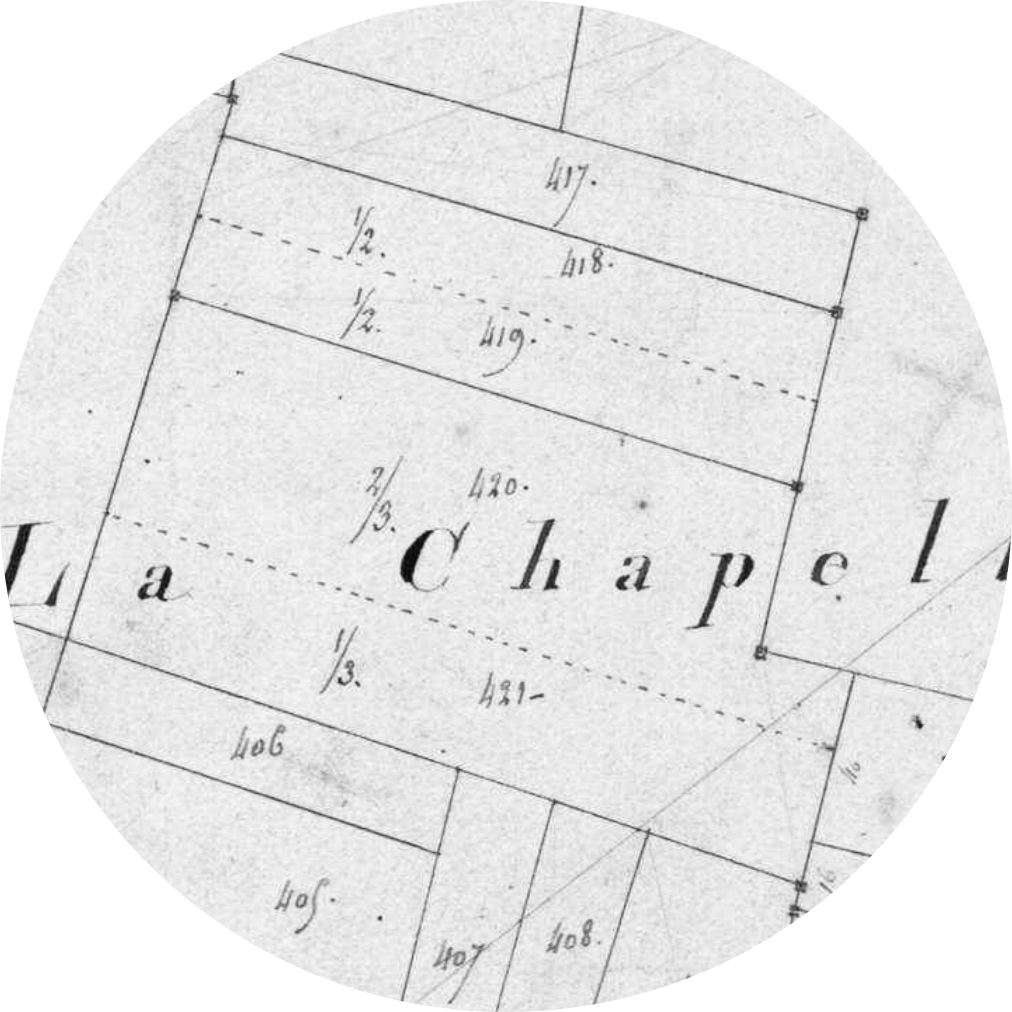
La lecture du travail de Barbotin nous a donné une occasion de découvrir le paysage d’Annappes en 1816. L’exploration des planches du cadastre permettrait de découvrir bien d’autres problèmes mathématiques que s’est posés le géomètre. On trouve par exemple le problème de la division des champs : les parcelles 420 et 421 de la section C2 sont la résultante d’un partage en deux tiers − un tiers d’un terrain (Fig. 10). À une toute autre échelle, la section B1 montre un partage organisé des marais en centaines de petites parcelles que l’on appelle parts de marais [note 15]. Par ailleurs, dans la section C2, on retrouve la trace du travail de l’ingénieur vérificateur avec la ligne de vérification tracée en bleu indiquant qu’une longueur de 2525,3 mètres mesurée sur le terrain correspond à une longueur sur le plan de 2521,0 mètres (soit une erreur de 1,7 m pour 1 km). Enfin, le lieu-dit « Les 7 Bonniers » que l’on trouve en section C1 rappelle que l’arrivée des géomètres du cadastre dans les campagnes est l’occasion pour l’État d’imposer le système métrique. La première page du tableau indicatif renseigne sur les conversions à effectuer : le bonnier d’Annappes vaut 1 hectare 41 ares, 86 centiares et 67 milliares.

Par cette exploration du cadastre de la commune d’Annappes, nous avons tenté de mettre en place des grilles de lectures, des pistes de travail pour une interprétation géométrique de la production sociale qu’est le cadastre napoléonien. Les transposer dans d’autres communes serait tout aussi fécond. Délimitations, bornages, canevas, parcelles, lignes de vérifications sont autant d’objets mathématiques qui nous renseignent sur le travail du géomètre.

À Annappes, l’analyse du canevas fait ressortir des principes généraux et des singularités de l’usage de la géométrie pratique. La permanence de ces méthodes fait de l’approche historique et mathématique du cadastre un outil pour l’enseignement. Comment lever un plan aujourd’hui ? Le géomètre-expert avec son théodolite s’appuie, avec des technologies modernes, sur les mêmes principes. Le levé de plan et plus généralement la géométrie du cadastre reposent fondamentalement sur l’étude des polygones quelconques et des figures semblables.

---

Notes

[1] (retour) Pour le cycle 3, il s’agit d’un travail sur les grandeurs et mesures, d’une première approche des figures usuelles (triangles et rectangles) et du plan, explicitement mentionné dans les programmes. Au cycle 4, il est possible de pousser le raisonnement sur la proportionnalité en lien avec les triangles semblables.

[2] (retour) Collectif, Manuel d’arpentage pour les écoles primaires, Paris et Tours : Mame et De Gigord, non daté.

[3] (retour) Pour un manuel disponible en ligne, voir par exemple F. J.-O. P., Arpentage, levé des plans et nivellement, Paris et Tours : Mame et Poussielgue, 1875.

[4] (retour) Louis Lamotte, Traité élémentaire d’arpentage et de lavis des plans, suivi de la mesure des bois et des solides : ouvrage destiné aux écoles communales supérieures et élémentaires et aux Propriétaires, Paris : Hachette, 1834, p. 78.

[5] (retour) F. J.-O. P., Arpentage, levé des plans et nivellement, op. cit., p. 27.

[6] (retour) Pour plus de renseignements sur l’histoire du cadastre, nous renvoyons à André Maurin, Le cadastre en France : histoire et rénovation, Paris : CNRS Éditions, 1990.

[7] (retour) Les archives départementales du Nord mettent à disposition les planche cadastrales numérisées de la plupart des communes du département.

[8] (retour) AD Nord, 24 / 2, État nominatif du premier germinal an XII (non paginé).

[9] (retour) Le programme du cours de Paris a été imprimé sous le titre Cours d’arithmétique, de géométrie et de géodésie ouvert le 27 Nivôse an XII. Voir Matthieu de Oliveira, « Un nouveau corps de fonctionnaires techniciens : les ingénieurs et géomètres du cadastre, 1800-1830 », dans De l’estime au cadastre en Europe. Les systèmes cadastraux au XIXe et XXe siècle, sous la dir. de Flo-
rence Bourillon, Pierre Clergeot et Nadine Vivier, Paris : CHEFF, 2008, p. 175-190.

[10] (retour) AD Nord, 24/2, arreté du 6 juin 1817.

[11] (retour) AD Nord, 24/1, Lettre du 9 mars 1807 du ministre au préfet.

[12] (retour) Les planches sont disponibles sur le site des archives du Nord. Les canevas, reconstitués par les auteurs et proposés sous forme de présentation dynamique pour le présent article, sont disponibles sur le site boutisses.free.fr.

[13] (retour) Les tours carrées de nombreuses églises du Nord devaient permettre d’installer le matériel du géomètre. On en a la certitude pour le cadastre de Seclin dressé par Barbotin en 1812 dont l’église est indiquée en section B1 comme étant aussi relais du télégraphe.

[14] (retour) Ce schéma est reproduit par le géomètre Dumelz en 1825 pour la petite commune voisine de Forest-sur-Marque, ce polygone constituant à lui seul la totalité du canevas (disponible sur boutisses.free.fr).

[15] (retour) Marc Fourdrignier, « Les portions ménagères de marais dans le nord de la France. Les exemples d’Ennevelin et Annappes », Revue du Nord 65, n°258 (1983), 555-566.