Auteur : Odile Guillon, Emmanuel Ostenne

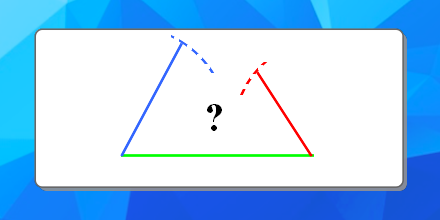
Faire découvrir aux élèves les inégalités triangulaires. L’activité propose de choisir, au hasard, trois nombres entiers compris entre 1 et 15 puis de construire si possible le triangle dont les trois nombres choisis sont les mesures de ses côtés en centimètres. Elle propose aussi d’étudier la fréquence des triangles constructibles.

Déroulement

• lieu : salle de classe
• durée : 40 minutes pour les constructions et la correction
• organisation : travail individuel sur feuille blanche puis bilan en classe entière
• matériel enseignant : un ordinateur et un vidéoprojecteur
• matériel élève : règle graduée, compas

But

• Découvrir l’inégalité triangulaire
• Objectifs :
  • tracer un triangle ;
  • observer et raisonner pour trouver les configurations dans lesquelles un triangle est constructible ;
  • calculer des fréquences.

Prérequis

• savoirs : connaître la notion de fréquence.
• savoir-faire :
  • construire un triangle connaissant les longueurs des trois côtés ;
  • calculer une fréquence.

Variantes

• Cette activité peut être reprise en troisième, la probabilité qu’un triangle soit constructible lorsqu’on choisit, au hasard, les longueurs des côtés du triangle parmi les nombres entiers de 1 à 15 peut alors être calculée à l’aide d’un tableur.

Documents

Archive de la construction avec InstrumenPoche (en local ou en ligne via le fichier texte triangle.xml) :

Simulation de 5 000 choix de 3 longueurs et calcul des fréquences des triangles constructibles et non constructibles :

Simulation de 5 000 choix de 3 longueurs et visualisation graphique de l’évolution de la fréquence des triangles constructibles en fonction du nombre d’expériences :

Tableur : Calcul de la probabilité qu’un triangle soit constructible lorsqu’on choisit les longueurs entières des côtés entre 1 et 15.

_{Transfert par E.O.}