Auteur : Pierre Lapôtre
Publication initiale : 2009

Exemple de programmation avec Xcas pour extraire la racine carrée d’un nombre. Prolongement en exercice classique.

Déroulement

• Lieu : salle informatique
• Durée : 1 heure + exercice à la maison
• Organisation : ordinateur disposant du logiciel gratuit Xcas (en ligne)

But

• Observer, apprécier la rapidité de convergence d’une suite.
• Intérêt pédagogique : algorithmique, programmation élémentaire.

Prérequis

• Savoirs : cours de 1ère S sur les suites.
• Savoirs-faire : algorithmique , utilisation de Xcas (élémentaire)

Commentaire

• Cette méthode d’extraction de la racine carrée d’un entier est connue sous le nom d’algorithme de Babylone ou algorithme de Héron (Héron d’Alexandrie, 1er siècle de notre ère).
• Elle peut être prolongée pour extraire la racine n-ième d’un nombre.
• Il s’agit de cas particuliers de la méthode de Newton pour obtenir un zéro d’une fonction f dérivable sur un intervalle I, dont la dérivée ne s’annule pas sur I : on considère la suite définie par récurrence, par :

 Elle peut être prolongée pour extraire la racine n-ième d’un nombre.

 Il s’agit de cas particuliers de la méthode de Newton pour obtenir un zéro d’une fonction f dérivable sur un intervalle I, dont la dérivée ne s’annule pas sur I : on considère la suite définie par récurrence, par :

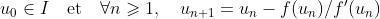
Le cas de l’algorithme de Babylone correspond à f(x)=x²-a

Documents

_{Transfert par E.O.}