Trigonométrie sans calculatrice

Auteur : Bernard Godon
Publication initiale : 2005

Avec des outils « rudimentaires » être capable de trouver des valeurs approchées des rapports trigonométriques, avoir une image mentale pour ces nombres et découvrir les premières propriétés.

Déroulement

Lieu : salle de classe
Durée : 1 heure
Organisation : Les élèves travaillent seuls puis en groupes de deux.
Matériel enseignant :
- projection des différents documents;
- transparent de correction.
Matériel élève :
- le matériel de géométrie : rapport, compas ;
- papier millimétré et tableau vierge.

Cadrage de l’activité

Présenter l’intérêt de cette belle activité (avec des outils « rudimentaires » être capable de trouver des valeurs approchées des rapports trigonométriques, donner une image mentale pour ces nombres et découvrir les premières propriétés).
La projection est un élément indispensable de cette activité.

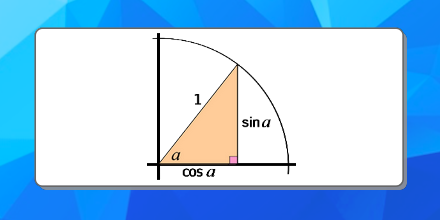
Faire tracer le quart de cercle de rayon 1 dm, en bas et à gauche de la feuille de papier millimétré (format portrait).
Faire ranger les calculatrices.
Montrer au rétroprojecteur la méthode pour obtenir, par exemple, cos 20°, sin 20° et tan 20° (valeurs approchées au centième).
Faire remplir les trois premières lignes du tableau.
Par deux, faire comparer les résultats.
Correction avec un transparent.
Faire conjecturer que pour des mesures d’angles croissants de 0° à 90° :
- le cosinus décroît de 1 à 0
- le sinus croît de 0 à 1
- la tangente croît de 0 à l’infini
- cos (90° – a )= sin a
- sin (90° – a )= cos a
- sin 45° = cos 45°
Avec la calculatrice compléter les deux dernières lignes.
Faire conjecturer que cos² a + sin² a = 1
(le démontrer en appliquant le théorème de Pythagore dans le triangle rectangle du quart de cercle).
faire conjecturer que tan a = sin a / cos a

But

Intérêt pédagogique : donner du sens aux nombres sin a, cos a et tan a et découvrir leurs premières propriétés.
Intérêt didactique : les élèves manipulent et peuvent comparer leurs résultats.