Auteur : Bernard Godon, Fabrice Eudes
Publication initiale : mai 2005

Séquence complète, avec documents pour les élèves et le professeur, pour découvrir la propriété de Pythagore et sa réciproque.

Déroulement

• Lieu : salle de classe
• Durée : 4 heures
• Organisation : alternance de travail individuel et de travail en groupe
• Matériel professeur :
  • prévoir les photocopies des différentes fiches ;
  • fabriquer les pièces du puzzle ( il doit pouvoir être montré au rétroprojecteur) ;
  • fabriquer le cordeau égyptien.
• Matériel élève :
  • quelques crayons de couleur ;
  • une calculatrice.

But : intérêt pédagogique

• Étape 1 : le test « longueur et aire »
  • approche naturelle de la notion de racine carrée d’un nombre positif. D’après les historiens, c’est de cette façon qu’elle apparut aux pythagoriciens. Les élèves découvrent la notion de nombre irrationnel à partir d’activités simples et de concepts qu’ils connaissent déjà ;
  • à l’occasion de l’introduction de la racine carrée, les élèves sont amenés à s’interroger sur les limites de la calculatrice.

• Étape 2 : le papier pointé
  • les élèves découvrent le théorème par eux-mêmes, l’enseignant
    crée des conditions favorables à son apprentissage.

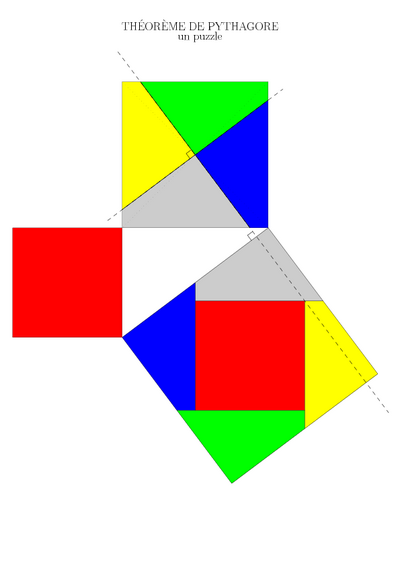
• Étape 3 : le puzzle
  • après l’étape n°2, qui a le même but, les élèves renforcent la même image mentale. En outre, ils découvrent le théorème par une activité différente, faisant appel à la manipulation.

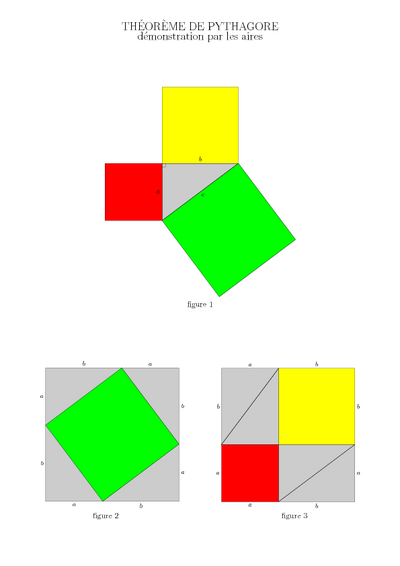
• Étape 4 : la démonstration
  • les trois démonstrations, choisies parmi toutes celles qui sont possibles, ont leur interêt :
    • la démonstration par les aires est l’une des plus simples et vient naturellement à la suite des séquences précédentes ;
    • la seconde démonstration utilise le calcul littéral et permet de travailler ce point important du programme ;
    • la démonstration par le cosinus est l’occasion de réinvestir une notion ancienne (la proportion) et une notion nouvelle (le cosinus).
  • l’initiation à la démonstration est un point important du programme de 4ème.

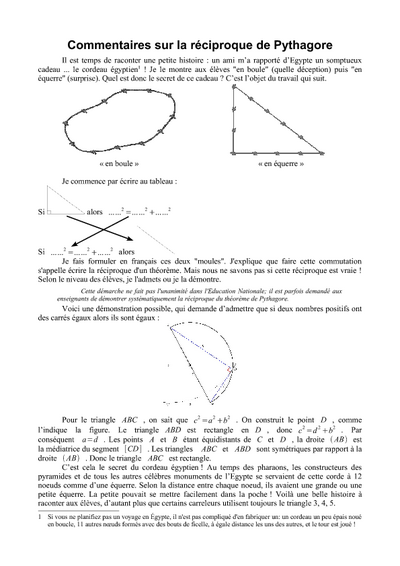
• Étape 5 : la réciproque
  • l’introduction à la réciproque du théorème de Pythagore est faite d’une façon vivante, à partir d’un objet tiré de la civilisation égyptienne.

• Étape 6 : les trois visages de Pythagore
  • la confusion entre théorème direct, la réciproque et la contraposée est un problème récurrent de l’enseignement des mathématiques, même au niveau supérieur. Il est important de l’aborder très tôt dans la scolarité.

But : objectifs

• Étape 1 : le test « longueur et aire »
  • évaluation des connaissances des quadrilatères, de la notion de carré, d’aire et de périmètre ;
  • évaluation des connaissances de la notion d’aire ;
  • introduction de la racine carrée (sa nature irrationnelle et sa définition).
• Étape 2 : le papier pointé
  • permet aux élèves de conjecturer le théorème de Pythagore.
• Étape 3 : le puzzle
  • permet aux élèves de conjecturer le théorème de Pythagore.
• Étape 4 : la démonstration
  • initiation à la démonstration. Trois démonstrations au choix sont proposées :
    • la démonstration par les aires ;
    • la démonstration littérale ;
    • la démonstration par cosinus.
• Étape 5 : la réciproque
  • introduire la réciproque du théorème de Pythagore ;
  • démontrer la réciproque du théorème de Pythagore (dans les classes dont le niveau le permet).
• Étape 6 : les trois visages de Pythagore
  • montrer la différence entre théorème direct, la réciproque et la contraposée ;
  • apprendre aux élèves à analyser les données d’un problème en vue de déterminer s’ils vont utiliser le théorème direct, la réciproque ou la contraposée ;
  • apprendre aux élèves à rédiger différemment selon qu’ils utilisent le théorème direct, la réciproque ou la contraposée. Remarque : un document à usage du professeur est proposé, qui met en évidence la confusion qui peut se faire entre théorème direct, la réciproque et la contraposée.

Prérequis

• Savoirs : la notion d’aire (les connaissances sur cette notion sont évaluées dans la première étape).

Références

• Curiosités géométriques : E Fourrey, Vuibert et Nony éditeurs, Paris, 1907 ;
• Dictionnaire des mathématiques : Stella Baruk, Le Seuil ;
• Py,Pytha, Pythagore : A. Deledicq, Collection Maths pour tous, vol 3, éditions ACL ;
• Repères IREM n°1, 5, 15 et 17 : éditions Topiques, Pont- A – Mousson ;
• Document d’accompagnement du programme de mathématiques : Françoise Vandieren, src Licap, Bruxelles.

Documents

• Étape 1 : le test « longueur et aire »

• Étape 2 : le papier pointé

• Étape 3 : le puzzle

• 4a. La démonstration par les aires

• 4b. La démonstration littérale

• 4c. La démonstration par cosinus

• Étape 5 : la réciproque

• Étape 6 : les trois visages de Pythagore

_{Transfert par E.O.}